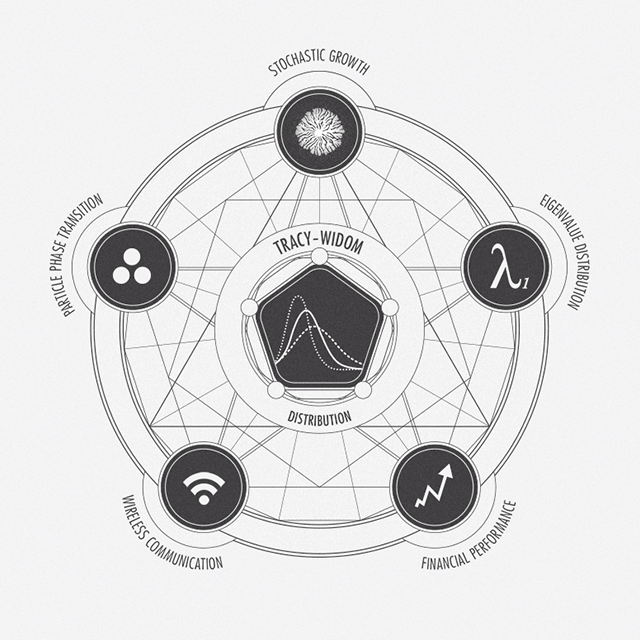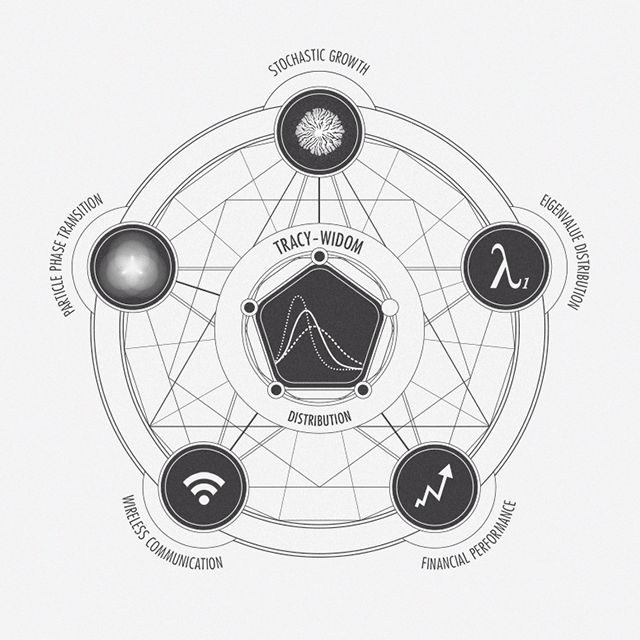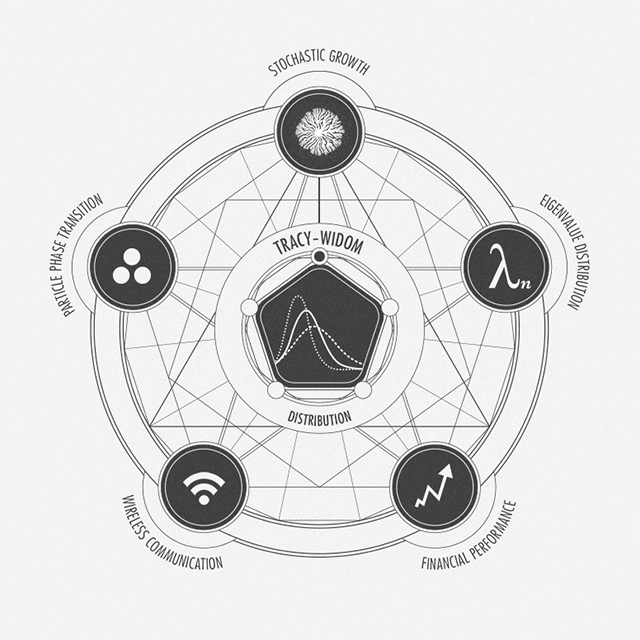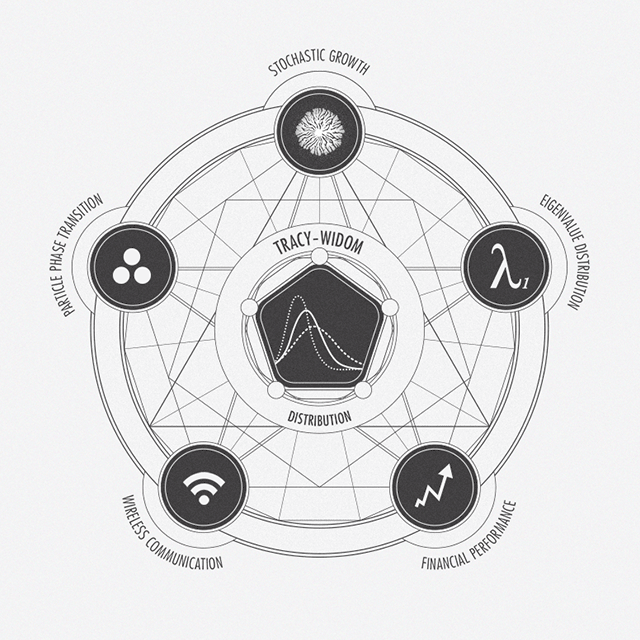
Tracy-Widom everywhere!
Natalie Wolchover from Quanta Magazine wrote great article about Tracy-Widom distribution, it’s history and it’s essence. TW distribution pretends to be a new universal law as it arises in many different classes of problems. It’s like Gaussian distribution, just slightly complex and asymmetric.
A small except from article:
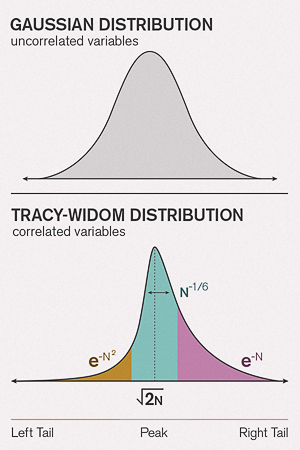 Systems of many interacting components — be they species, integers or subatomic particles — kept producing the same statistical curve, which had become known as the Tracy-Widom distribution. This puzzling curve seemed to be the complex cousin of the familiar bell curve, or Gaussian distribution, which represents the natural variation of independent random variables like the heights of students in a classroom or their test scores. Like the Gaussian, the Tracy-Widom distribution exhibits “universality,” a mysterious phenomenon in which diverse microscopic effects give rise to the same collective behavior. “The surprise is it’s as universal as it is,” said Tracy, a professor at the University of California, Davis.
….
The central limit theorem, which was finally made rigorous about a century ago, certifies that test scores and other “uncorrelated” variables — meaning any of them can change without affecting the rest — will form a bell curve. By contrast, the Tracy-Widom curve appears to arise from variables that are strongly correlated, such as interacting species, stock prices and matrix eigenvalues. The feedback loop of mutual effects between correlated variables makes their collective behavior more complicated than that of uncorrelated variables like test scores. While researchers have rigorously proved certain classes of random matrices in which the Tracy-Widom distribution universally holds, they have a looser handle on its manifestations in counting problems, random-walk problems, growth models and beyond.
Systems of many interacting components — be they species, integers or subatomic particles — kept producing the same statistical curve, which had become known as the Tracy-Widom distribution. This puzzling curve seemed to be the complex cousin of the familiar bell curve, or Gaussian distribution, which represents the natural variation of independent random variables like the heights of students in a classroom or their test scores. Like the Gaussian, the Tracy-Widom distribution exhibits “universality,” a mysterious phenomenon in which diverse microscopic effects give rise to the same collective behavior. “The surprise is it’s as universal as it is,” said Tracy, a professor at the University of California, Davis.
….
The central limit theorem, which was finally made rigorous about a century ago, certifies that test scores and other “uncorrelated” variables — meaning any of them can change without affecting the rest — will form a bell curve. By contrast, the Tracy-Widom curve appears to arise from variables that are strongly correlated, such as interacting species, stock prices and matrix eigenvalues. The feedback loop of mutual effects between correlated variables makes their collective behavior more complicated than that of uncorrelated variables like test scores. While researchers have rigorously proved certain classes of random matrices in which the Tracy-Widom distribution universally holds, they have a looser handle on its manifestations in counting problems, random-walk problems, growth models and beyond.
To be clear, this visualization nicely shows where Tracy-Widom distribution can arise :